Los hombres que miraban fijamente a los microondas

Un horno microondas calienta la comida mediante calentamiento dieléctrico: el agua contenida en los alimentos es una molécula polar —es decir, que su distribución de cargas eléctricas no es del todo simétrica. Por ello, reacciona vibrando y calentándose frente a un campo electromagnético variable. La frecuencia del campo no es muy importante: el microondas inicial, además de pesar 340 kg, medir 1,80 m de altura, costar 5000 pavos y necesitar una toma de agua y un sumidero para refrigerar su magnetrón, utilizaba radiofrecuencia de 10 a 20 MHz. El uso de la banda de 2,45 GHz en los microondas actuales es debido a que se trata de una banda libre de regulación en todo el mundo, en la que cualquiera puede emitir (una banda ISM) y en la que, por tanto, se pueden producir interferencias legalmente. Longitudes de onda mayores calentarían la comida a más profundidad, pero el equipo necesario para producirlas con la intensidad necesaria se encarece.

Así, tenemos un aparato fabricado por el contratista más barato (en la inmortal frase del astronauta Alan Shepard)  que emite alrededor de 700 W de radiación en la misma banda que el wifi, el bluetooth, los teléfonos DECT inalámbricos, los reemisores de televisión caseros… Ninguno de estos aparatos está diseñado para cocer nada (hoaxes de internet aparte), pero el horno microondas sí. La pregunta es inevitable: ¿por qué no nos cuece los globos oculares mientras miramos cómo da vueltas dentro nuestro plato de sopa?

La explicación

El microondas es una jaula de Faraday. Como los buenos conductores son opacos a la radiación de microondas, las paredes del horno, construidas de metal, reflejan y contienen el campo, asegurándose de que solo sea absorbido por lo que tiene que calentarse: la comida. ¿Os lo creéis? Repasemos la definición: una jaula de Faraday es una superficie conductora cerrada… ¡Espera! El interior del horno no es realmente una superficie cerrada. La puerta tiene unos agujeros para poder ver cómo se cocina nuestra magistral receta… ¿Qué ocurre de verdad?

La explicación de verdad

Vale, de acuerdo, el microondas es “casi” una jaula de Faraday, pero si la puerta fuera toda de metal no lo querríamos porque no podríamos ver si el chocolate de la taza que hemos metido se ha puesto a hervir y hay que estampar el puño en el botón de parada. La estructura de la puerta es una rejilla metálica con agujeros al tresbolillo. El truco aquí es que los agujeros, de alrededor de 2 mm de diámetro, son mucho más pequeños que la longitud de onda de la radiación de microondas que hay dentro. Veamos:

[latex]\lambda = \dfrac{c}{f}[/latex]

Donde c es la velocidad de la luz en el vacío y f la frecuencia de la onda electromagnética. Introduciendo los números obtenemos que λ = 122 mm, tres órdenes de magnitud por encima. Así pues, queda comprobado. Las microondas no “caben” por los agujeros de la puerta, mientras que la luz visible, con longitudes de onda de 400 a 700 nm —cuatro órdenes de magnitud por debajo del tamaño de los agujeros— pasa sin problemas. Por eso los microondas no nos cuecen los ojos. ¿Sí?

La explicación de verdad, de verdad

Bueno… ¿Os suena el concepto de difracción? Es un fenómeno curioso. Si suponemos que toda la radiación incide en la puerta del microondas de forma perpendicular —más que nada, por poner las cosas feas, porque toda onda que incida con un ángulo menor que 90º “verá” los agujeros más pequeños— lo que ocurre en realidad puede describirse muy bien con esta imagen:

Aquí las fórmulas empiezan a hacerse complicadas, así que para obtener una impresión intuitiva de lo que está pasando en la rejilla del horno conviene echarle un vistazo a esta aplicación: Wave2D. Se trata de un pequeño applet de Java que simula la difracción de una onda frente a diferentes tipos de obstáculos. Si bien no está pensada para reflejar el caso de un horno microondas, podemos obtener una idea aplicable a nuestro caso si ajustamos los controles del siguiente modo (en orden, de arriba abajo):

• Seleccionar Setup: Multiple Slits (rendijas múltiples) en la primera caja de selección.
• Show Intensity (mostrar intensidad) —marcado.
• Tri-Chromatic (tricromático) —sin marcar.
• Show Units (mostrar unidades) —marcado.
• Incidence Angle (ángulo de incidencia de la radiación) —a la mitad.
• Zoom Out (factor de alejamiento) —al mínimo.
• Resolution (resolución) —al máximo.
• Source Frequency (frecuencia de la fuente de radiación) —a la mitad.
• Brightness (brillo de la imagen resultante, o intensidad de la radiación) —a la tercera parte del total.
• Slit count (número de rendijas) —al máximo.
• Slit Width (ancho de las rendijas) —a dos terceras partes del total.
• Separation (separación de las rendijas) —al máximo.

La aplicación muestra una onda de luz visible incidiendo desde la parte superior de la pantalla en un plano con un conjunto de ranuras que, naturalmente, se ve de canto. Los bonitos patrones que se forman tienen su origen en la dispersión producida por cada ranura y en la interferencia entre todas ellas. Si cortáramos la rejilla de la puerta de un microondas según un plano perpendicular y representáramos la radiación filtrada, los patrones visibles se asemejarían a lo que muestra esta aplicación.

En la aplicación, la longitud de onda de la radiación tan solo varía entre λ = 650 nm (rojo) y λ = 475 nm (azul). Las anchuras de rendija y las separaciones disponibles son similares. Podemos ver el resultado de reducir la anchura de las rendijas para buscar una configuración proporcionalmente similar a un microondas —recordemos que en los hornos, la longitud de onda de la radiación es alrededor de 100 veces más grande que el diámetro de los agujeros. No lo conseguiremos, ya que el rango de valores admitidos por la aplicación no permite bajar de 200 nm para el ancho de rendija, lo que es más o menos la mitad de la longitud de onda más corta que se puede representar. Sin embargo, sí podemos empezar a apreciar el efecto de atenuación del campo.

Calcular exactamente el valor de la atenuación de la radiación del microondas que ofrece la puerta son palabras mayores. Podemos, eso sí, hacer aproximaciones conservadoras. Supongamos que el campo electromagnético incidente es una onda plana y que, en el peor de los casos, es perfectamente perpendicular a la puerta (no lo será: para empezar, el magnetrón está siempre a un lado —normalmente a la derecha— y las ondas se reflejarán una o más veces antes de intentar salir por la rejilla). En 1971, T.Y.Otoshi y K.Woo, del Jet Propulsion Laboratory, presentaron una fórmula relativamente sencilla para estimar la atenuación en decibelios de una placa perforada con agujeros circulares bastante más pequeños que la longitud de onda de la radiación —como es el caso. Yo la simplifico un poco más, suponiendo que la radiación incide de forma perpendicular a la rejilla:

[latex]T_{dB} \approx 20 \log_{10} \dfrac{3 a b \lambda_0}{2 \pi d^3} + \dfrac{32 t}{d} [/latex]

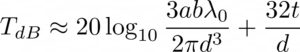
Donde t es el espesor de la rejilla y a, b y d son parámetros geométricos de los agujeros, según el siguiente diagrama:Suponiendo que a = 2,5 mm. d = 1,8 mm y t = 0,5 mm, obtenemos que T_dB = 44 dB. ¿Y eso es mucho? En general, sí, pero depende de la radiación que sea capaz de absorber y transformar en calor la comida que pongamos dentro. Una vez más, acudamos al peor de los casos: el del horno vacío. Si no hay nada para absorber parte de la radiación, para un microondas de 750 W, obtenemos una potencia en dBW de

[latex]P_{dBW} = 10 \log_{10} 750 = 28,75 \text{ dBW}[/latex]

Lo grande de operar en decibelios es que todo es sumar y restar (¡sí, chicos, ese es el secreto de Teleco, todo es sumar y restar! ¡Tienes que llegar a cuarto curso y superar unas pruebas que ríete de las de Astérix para que te lo revelen, pero es la verdad!) Así que la potencia transmitida al otro lado —al lado de nuestros ojos— es 28,75 − 44 = −15,33 dBW, y deshaciendo el logaritmo, aproximadamente de 29 mW a repartir por toda la superficie de la puerta. Si es de 30 × 15 cm, más o menos 65 µW/cm².

Entre nosotros, eso es una nonada. Una fruslería. Una insignificancia. Y además, es totalmente irrelevante… porque sale más radiación por los bordes de la puerta. ¿Por qué no nos cuece los ojos entonces el microondas?

La explicación de verdad, de verdad, de verdad de la buena

Sí, claro. En un microondas de verdad —ya hemos dejado muy atrás el mundo ideal y las frases del tipo “sea un microondas esférico”— la puerta se abre y se cierra. ¡Por eso hay una puerta! El detalle de poder ver a través de ella es secundario comparado con la capacidad, ya sabéis, de meter y sacar la comida. ¿Cómo hacen los fabricantes de microondas para no cocernos? Resulta que emplean un truco geométrico copiado de los empalmes de las guías de ondas. ¿Perdón?

La manera más fácil de imaginarse una guiaonda es pensar en la luz. La luz es radiación electromagnética, y se puede guiar con fibras ópticas. Pues bien, las microondas también pueden guiarse. El montaje es un poco más incómodo, pero muy sencillo. Una guía de onda (guiaonda para los amigos) es, normalmente, un tubo de metal. ¿Ya? Más o menos. Sólo tiene que ser buen conductor: los campos electromagnéticos, a las frecuencias de las microondas, se reflejan en los buenos conductores —nota para los que tengáis un seguro con la compañía aseguradora del erizo: no va por vosotros. El tubo contiene el campo estupendamente y actúa como una tubería de agua (bueno, luego están los modos de propagación, los dieléctricos internos… pero la base es esa). El problema llega cuando el tubo se acaba y no conviene soldar otro, porque habrá que desmontar el aparato algún día. Cualquier discontinuidad en el tubo provocará pérdidas que preferiríamos obviar. ¿Qué hacemos?

Usar una junta de estrangulación en λ/4, choke o “de choque” en mucha literatura —los ingenieros eléctricos y las traducciones, esos enemigos mortales. Básicamente se trata de una ranura con perfil en forma de U de una anchura aproximada de un cuarto de la longitud de onda que se pretende contener. Este montaje consigue que el campo electromagnético muestre un mínimo en el borde de la junta, reduciendo así las pérdidas. Los fabricantes de hornos han patentado variantes de este montaje, pero este es el motivo de que los bordes de las puertas tengan siempre unas dimensiones parecidas, rondando los 3 cm: ¡es la cuarta parte de 12 cm, la longitud de onda de la radiación!

¿Es eso todo?

Una puerta es una puerta. Una cocina dista mucho de ser un laboratorio donde los equipos se manejan con guantes —o con algo de cuidado. Así que si midiérais la intensidad del campo fugado del microondas, apuesto a que obtendríais el valor máximo alrededor de la puerta y no en su frente. La evolución del diseño de puertas en los hornos microondas ha pasado desde la solución obvia del contacto metálico, que no funciona tan bien como parece debido a las deformaciones propias del uso y, sí, a la suciedad, a las puertas actuales. Aunque existen otras aberturas en la “supuesta” jaula de Faraday (rejillas de ventilación, el eje del motor del plato giratorio…) el borde de la puerta sigue siendo el factor clave a la hora de estimar el campo de fugas de un microondas. Y sin embargo no puede cocernos los ojos. Las pérdidas típicas de un horno actual, nuevo, son del orden de 0,2 mW/cm², un orden de magnitud por debajo de lo que marca la norma de homologación —que es compatible con las recomendaciones de la OMS.

¿Seguro?

No. ¡Así somos los ingenieros! Nunca encontraréis nada “perfectamente seguro”: el mismo concepto de seguridad perfecta no tiene sentido. Sin embargo, os dejaré dos pequeñas listas de recomendaciones operativas para el uso y disfrute de la tecnología del microondas aplicada a la cocina de autor —palomitas, tazas de café, y similares.

Lista de recomendaciones estándar

Esta lista es de aplicación para todas aquellas personas que quieran vivir tranquilas en su entorno actual, buscando el punto óptimo entre la seguridad y la conveniencia. También vale para los que pasen de todo, pero no quieran ganar un premio Darwin por descuido:

• No permanezcáis un tiempo innecesario cerca de un microondas en marcha. “Cerca” significa “a pocos centímetros”. La radiación de fugas disminuye muy rápido, y un metro es una distancia segura (para tranquilidad de los que tenemos cocinas microscópicas).
• No encendáis el microondas en vacío, con algo que no sea un alimento o que no contenga agua, o con un alimento totalmente envuelto en papel de aluminio. Si no hay nada dentro, o lo que hay no absorbe energía (una piedra, un vaso vacío, vete a saber qué tonterías pueden ocurrírsele a una mente ociosa), se escapará más radiación. Por lo menos mientras el magnetrón no arda por el exceso de energía reflejada que no puede disipar por sus propios medios (debería saltar antes un fusible, pero mejor no probéis).
• No uséis un microondas con la puerta dañada. Hay que hacer bastante el bestia para cargarse la puerta de un microondas, y aún así, si no funciona el cierre, hay un interruptor de interbloqueo que no permite que el magnetrón se ponga en marcha. Pero si la puerta está un poco rota podría no actuar adecuadamente. Hacéos un favor y llevadlo al punto limpio más cercano: los microondas nuevos no son tan caros.

Lista de recomendaciones especial

Esta lista se la dedico a todos los amigos de vuestros amigos que estén afectados en algún grado por la fobia electromagnética, y a los empleados de Geosanix, la fundación VivoSano y otros engendros afines para que alcancen la tranquilidad de ánimo que buscan unos, y nuevas ideas de negocio otros:

• ¿Todavía tenéis microondas? Tiradlo. Lejos. Es hora de redescubrir los beneficios de la cocina con leña. Nota: cocinar con leña ardiendo puede provocar quemaduras graves. En caso de duda, preguntad por Juana de Arco. Ella, eso sí, tuvo el beneficio de ver con sus propios ojos los efectos de las llamas, cosa que las malvadas microondas nunca nos permitirán.
• Consigue que tiren también el microondas todos tus vecinos, porque no importa la intensidad del campo al que puedas verte expuesto —lo importante es que hay radiación. Bonus si consigues que tu ayuntamiento declare el pueblo “zona libre de microondas”.
• Cualquier cosa parecida a un emisor de microondas debe desaparecer. Esto incluye, pero no está limitado a: teléfonos inalámbricos, equipos de wifi, teléfonos móviles y sus antenas base, televisores y repetidores de televisión, transistores, antenas emisoras de radio, etcétera. Todos estos artefactos del demonio funcionan en bandas similares y seguro que nos están matando. Mirad si no cómo se le derritió la cara a Belén Esteban (ah, ¿que no se le derritió?)
• Dicen que poner internet por los cables de la electricidad (PLC) es seguro. Mienten: la red de distribución doméstica, que no va apantallada, se convierte en antenas gigantes que irradian campos de alta frecuencia. Vais a morir igual, y además os habrán sacado antes más dinero.
• Si no conseguís todo lo anterior, tendréis que confeccionaros una jaula de Faraday portátil. Mi recomendación es que os cubráis todo el cuerpo (todo) con una capa de pan de oro doble, conectada eléctricamente a una toma de tierra de buena calidad para evitar la acumulación de cargas. No os mováis mucho para no romperla.
• Las cortinas antirradiación son una ayuda, pero las paredes solo suelen atenuar la banda de microondas en 3 dB (a la mitad, para los no-telecos entre la audiencia). Blinda también las paredes. Hay rejillas de protección que se venden por metros y se pueden aplicar como papel pintado para conseguir una apariencia a la última moda magufa. Ten a mano unos cuantos miles de euros, y no te olvides del suelo, el techo y las puertas.
• Si, pese a todo, decides marcharte a vivir a una cueva, ten en cuenta que las emisiones naturales de gas radón no son ninguna tontería. Vivir es poder morirse.

---

Esta entrada participa en el VI Carnaval de la Tecnología celebrado este mes en Scientia.

Bibliografía:

Wave2D, © 2004 Paul Falstad. Instrucciones de uso detalladas, y código fuente para enredar.

A Study of Microwave Transmission Through Perforated Flat Plates, T.Y.Otoshi, JPL Technical Report 32-1526, vol. II, 1971.

Simulation of Electromagnetic Leakage from a Microwave Oven, A.M.Rocha, M.Facão, J.P.Sousa, A.Viegas, Proceedings of EHE’06, 1.29-1.34, 2006.

Microwave Ovens and their Hazards, Canadian Center for Occupational Health and Safety, noviembre 2004.

Campos electromagnéticos y salud pública: Hornos microondas. Hoja informativa, OMS, febrero 2005.

UNE-EN 60335-2-90:2007. Aparatos electrodomésticos y análogos. Seguridad. Parte 2-90: Requisitos particulares para hornos microondas comerciales. (IEC 60335-2-90:2006)