Medir es comparar con un patrón relevante. Podemos estar más o menos seguros de que entendemos ese concepto básico de la medida. Kilos de patatas, metros cuadrados de vivienda, litros de leche. Pero no kilos de vivienda, metros cuadrados de leche o litros de patatas, salvo que retorzamos alegremente las definiciones. Sin embargo, hay hechos bastante cotidianos que no tienen patrones de medida tan intuitivos. Hoy hablaré del transporte: ¿cómo comparar el rendimiento de diferentes medios, vehículos o trayectos? La longitud recorrida, el tiempo transcurrido o la masa transportada nos da pistas, pero no nos ofrece una visión global del fenómeno. En otras palabras, necesitamos algún modo de medir su utilidad. Lo que «produce» un avión, un coche o un tren. Idealmente, la unidad que empleemos tendrá que servir igual para todos los modos de transporte. Una vez hayamos resuelto este enigma, no nos costará demasiado lanzarnos a averiguar más detalles escabrosos sobre los diferentes medios de transporte: cuánto cuestan por unidad producida, cuánta energía consumen o, también, la cantidad de emisiones de gases de efecto invernadero que genera cada uno.
Necesitamos encontrar una unidad de medida relevante para una magnitud. ¿De qué pistas disponemos? Un avión, por ejemplo, transporta pasajeros. Así que la cantidad de estos tendrá que formar parte de la medida. Por otro lado, ese mismo aparato recorre distancias por el aire, así que los kilómetros saldrán por algún lado. Si lo que deseamos es ser capaces de conocer la «producción» del avión en alguna «unidad de transporte», parece claro que más pasajeros equivale a más producción —y más kilómetros también—. ¿Qué es «más transporte» entonces, mover cuatro personas 100 kilómetros, o 100 personas cuatro kilómetros? ¿Y si multiplicamos una cosa por la otra?
4 pasajeros × 100 kilómetros = 400 p·kmO bien…
100 pasajeros × 4 kilómetros = 400 p·km¡Son lo mismo!
El pasajero-kilómetro es una magnitud que normaliza diferentes distancias y personas transportadas. Así podemos comparar trayectos e, incluso, distintos medios de transporte. El mismo truco funciona también para el transporte de mercancías. Solo hay que cambiar los «pasajeros» por alguna unidad significativa para lo que quiera que estemos transportando. Por ejemplo, toneladas.
Solemos tener problemas con las unidades compuestas que se multiplican, así que el pasajero-kilómetro es una unidad «difícil». Le pasa lo mismo al vatio-hora, más conocido por su múltiplo kilovatio-hora (kW·h) en los recibos de las compañías eléctricas: el vatio, unidad de potencia, va multiplicado por la hora, unidad de tiempo. El resultado es una unidad de trabajo o energía, porque la potencia se define como un trabajo desarrollado en cierto tiempo.
[potencia] × [tiempo] =
[trabajo] / [tiempo] × [tiempo] =
[trabajo]Sin embargo, estamos tan acostumbrados a que las unidades compuestas nos cuenten historias de reparto de una cosa en otra (ocurre con la potencia, o con la misma velocidad, que es una longitud dividida por unidad de tiempo) que, sin darnos cuenta, cometemos una y otra vez el error de hablar de «kilovatios partidos por hora» o «pasajeros partidos por kilómetro». Eso es un error, pero no porque las unidades no tengan sentido. Seguramente habrá algún hecho físico que puedan describir. En el primer caso estaríamos hablando de un trabajo dividido por tiempo al cuadrado, que podría ser, por ejemplo, una unidad para expresar la tasa de cambio de la potencia. En el segundo, podríamos imaginarnos describiendo así los pasajeros que suben o bajan de un autobús a lo largo de un kilómetro de su trayecto. El fallo, entonces, está en usar unidades que expresan algo diferente de lo que queríamos decir: trabajo y capacidad de transporte, respectivamente.
Hay dos maneras diferentes de fijar en nuestras mentes el concepto de pasajero-kilómetro. Uno es pensar que, después de todo, no es tan raro multiplicar dos unidades para conseguir una unidad compuesta. Solo hay que pensar que la superficie se mide en metros cuadrados, que no es más que metros multiplicados por metros. El pasajero-kilómetro puede verse como una forma extraña de «superficie», aunque una en la que cada una de sus dos dimensiones se mide de manera diferente: una en número de personas y la otra en kilómetros.
Otra manera, bastante intuitiva, es pensar en alguna unidad derivada que tenga el pasajero-kilómetro dividiendo. Considerad el siguiente gráfico:
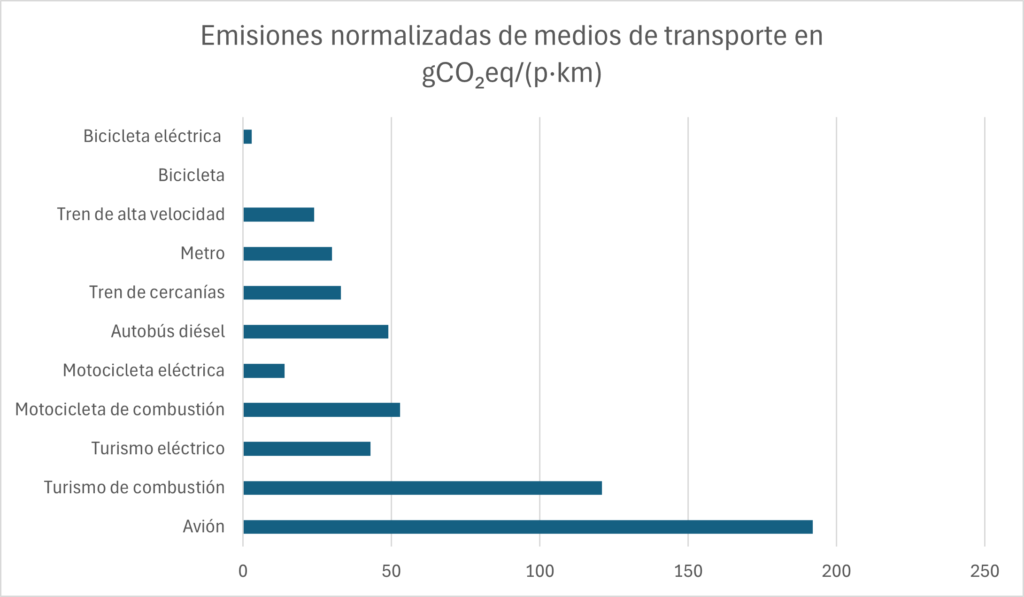
Si queremos comparar medios de transporte respecto de sus emisiones, medidas en gramos de dióxido de carbono1, tenemos que igualar en la medida de lo posible la base de la comparación. Hacerlos recorrer la misma distancia (un kilómetro) y transportando a los mismos pasajeros (uno) parece lo más razonable. Si recorremos más distancia y con más gente, podemos dividir por los dos valores las emisiones totales. Y, por la aritmética elemental, dividir por dos valores a la vez equivale a multiplicarlos primero.
(gCO₂/km)/p = gCO₂/(p·km)El concepto de pasajero-kilómetro (o su equivalente de tonelada-kilómetro para el transporte de cargas) es absolutamente fundamental en la ingeniería del transporte. Nos permite comparar diferentes trayectos, e incluso diferentes medios, para extraer conclusiones constructivas acerca de su eficacia. No refleja toda la historia. De otro modo, sería posible defender la sustitución de todos los trayectos en avión por bicicletas. Pero es una herramienta clave en la comprensión del transporte como fenómeno clave no ya en la economía, sino en la experiencia humana.
- El sufijo «eq» que aparece en la unidad del gráfico indica «equivalente». Es nuestra forma de decir que no consideramos solo emisiones directas, sino también aquellas imputables a la existencia del medio de transporte, como las necesarias para fabricarlo, desguazarlo al final de su vida o alimentarlo durante su funcionamiento habitual. ↩︎


Comentarios
2 respuestas a «¿Cuánto pesa el transporte?»
@blog cómo me gusta esta mierda..
Bueno… A ti precisamente era de esperar 😉.